Криптовалюта Binarium
Введение
Бинариум – первая защищённая от ASIC криптовалюта. Ее защита создана с помощью конфигурируемого хэширующего алгоритма (с использованием различных хэширующих и шифрующих подфункций), который перестраивается раз в неделю или в случае изменения сложности генерации блоков. Это делает дорогими покупку ASIC для каждой подфункции и их переконфигурацию в соответствии с текущим состоянием алгоритма. Он также использует амплификацию данных с помощью быстрой поточной шифрующей функции Salsa20[9], это делает хэширование зависимым от размеров оперативной памяти и кэшей и скорости произвольного доступа к данным. Что ещё больше увеличивает стоимость создания ASIC для такой криптовалюты и уменьшает эффективность GPU в майнинге, так как их видеопамять больше подходит для конвеерных передач больших объёмов данных, вместо скорости произвольных доступов к ней, и так как их кэш используется несколькими ядрами одновременно и часть из него доступна только для чтения. При этом каждый поток, вычисляющий хэши блоков Бинариума, должен обладать своей областью памяти для записи данных, так как процессы вычисления и промежуточная информация зависят от начальных данных рассматриваемого блока. Главной особенностью, защищающей криптовалюту от ASIC, является возможность менять хэширующие функции после широкого применения Бинариума, сохраняя при этом его текущий консенсус.
Бинариум — первая криптовалюта, которая поддерживает изменение хэширующих функций и внесение других крупных изменений в сеть с сохранением текущего консенсуса. Это делается с помощью процесса, состоящего из 4-х шагов: введение неактивных обновлений в программное обеспечение; «мягкое» форсирование клиентами друг друга к обновлению; «жёсткое» форсирование клиентами друг друга к обновлению; и сама активация обновлений в пирах, когда сеть сообщает о достаточном уровне применения новых функций. В этой модели клиенты отправляют на главный RPC-сервер Бинариума статистическую информацию о количестве обновившихся пиров, с которыми у них установлена связь. Это позволяет определять текущее состояние сети и активировать изменения, когда достаточное количество пользователей обновят их программное обеспечение. Данная функциональность будет реализована после запуска криптовалюты, при достаточной обратной связи о работе текущего алгоритма хэширования и общем функционировании block-chain-сети Бинариум.
Она также основывается на криптовалюте Dash[2] и наследует master nodes, InstantSend и PrivateSend от неё.
Мы планируем ввести интеграцию Бинариума с онлайн-играми в следующей форме:
- Внутриигровая валюта, которую игроки могут покупать и продавать за реальные деньги.
- Внутриигровые и околоигровые квесты, создаваемые разработчиками компьютерных игр, которые игроки могут выполнять и получать награду в Бинариуме.
- Торговые соглашения между игроками, с которых разработчики игр и разработчики Бинариума будут получать комиссию.
- Биржа для торговли играми, DLC, внутриигровыми вещами, внутриигровыми деньгами и другими ценностями.
- Возможность организовывать турниры разработчиками игр и самими игроками с призами в Бинариуме, а также в виде игр, DLC, внутриигровых предметов и других ценностей. Впоследствии мы планируем добавить к криптовалюте умные контракты, электронный документооборот и другие функции, которые мы пока будем держать в секрете. Мы предоставим дальнейшие технические детали о реализации функций в следующих секциях, также вы можете увидеть всё сами в исходном коде Бинариума[14].
1. Разнообразие алгоритмов и переконфигурация
1.1. Хэширующие алгоритмы
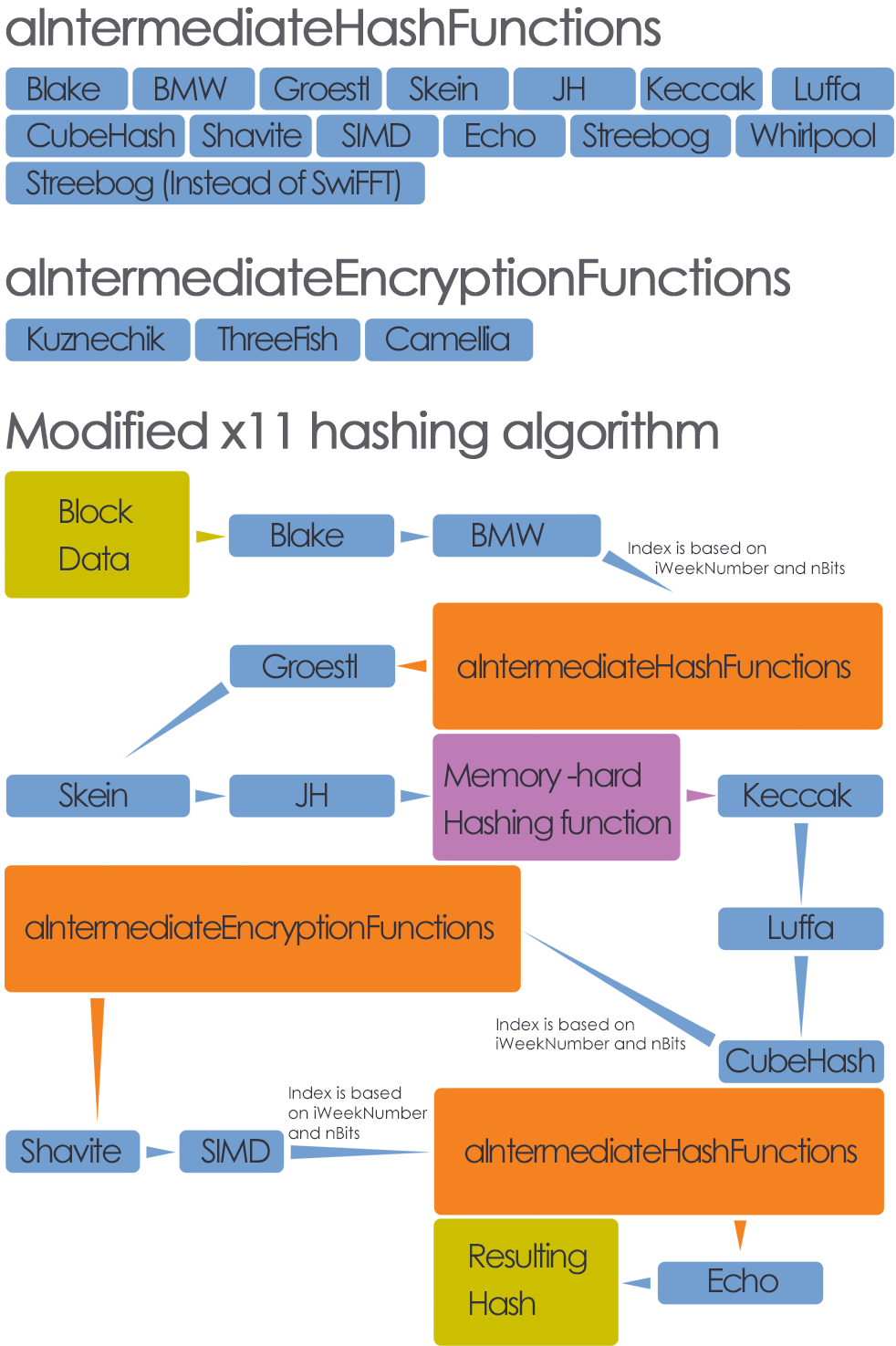
Хэширующий алгоритм Бинариума базируется на X11[2], он использует его хэширующие подфункции: blake, bmw, groestl, skein, jh, keccak, luffa, cubehash, shavite, simd и echo. Также были добавлены следующие функции: российская ГОСТ 2012 Стрибог[3] и Whirlpool [4]. Мы рассматривали возможность добавления хэширующей функции SwiFFT [5], которая использует Быстрые Преобразования Фурье[15] для генерации хэшей из начальных данных и, возможно, может быть использована в эру Постквантовой Криптографии[13]. Но эта функция сейчас довольно сырая и используется не так широко, поэтому лучше всего отложить её для последующей проработки и рассмотреть её реализацию в следующих крупных обновлениях сети.
1.2. Шифрующие алгоритмы
Бинариум также использует надёжные криптографические шифрующие функции в процессе вычисления хэшей: блочный шифр ГОСТ 2015 Кузнечик[6], блочный шифрующий алгоритм ThreeFish [7] и блочный шифр Camellia[8].
1.3. Реконфигурация каждую неделю и с каждым изменением сложности вычислений создания блоков сети
В процесс вычисления хэша X11 внесены три расчета конфигурируемых хэширующих и шифрующих функций. Они определяются по номеру недели со времени создания Genesis-блока и полю nBits текущего блока. Первая функция после второго шага, между вычислениями хэшей BMW и Groestl:
iWeekNumber = _iTimeFromGenesisBlock / I_ALGO_RECFG_TIME_PERIOD_IN_SECONDS * I_ALGO_RECFG_TIME_PERIOD_IN_SECONDS;
iIndex = (iWeekNumber + nBits) % I_AMOUNT_OF_INTERMEDIATE_HASH_FUNCTIONS;
aIntermediateHashFunctions[iIndex](uint512AdditionalHash.begin(), 64, nullptr, static_cast(&hash[1]));
Этот код выбирает хэширующую функцию из массива доступных и применяет её к промежуточному хэшу. Вторая функция после шага восемь хэширования X11, между применением подфункций CubeHash и Shavite:
iIndex = (iWeekNumber + nBits) % I_AMOUNT_OF_INTERMEDIATE_ENCRYPTION_FUNCTIONS;
aIntermediateEncryptionFunctions [iIndex] (
static_cast(&hash[6]), 64, static_cast(&hash[0]), static_cast(&hash[7])
);
Этот код выбирает шифрующий алгоритм из массива доступных и применяет его к промежуточному хэшу. Третий конфигурируемый шаг внесён между 10-м и 11-м шагами — между применением подхэшей SIMD и Echo :
iIndex = (iWeekNumber + nBits + 10) % I_AMOUNT_OF_INTERMEDIATE_HASH_FUNCTIONS;
aIntermediateHashFunctions[iIndex](uint512AdditionalHash.begin(), 64, nullptr, static_cast(&hash[9]));
Он выбирает хэширующую функцию из массива с отступом относительно первого индекса переконфигурации.
2. Хэширующая функция, основанная на псевдопроизвольных чтении и записи данных в память
2.1. Последовательная Salsa20
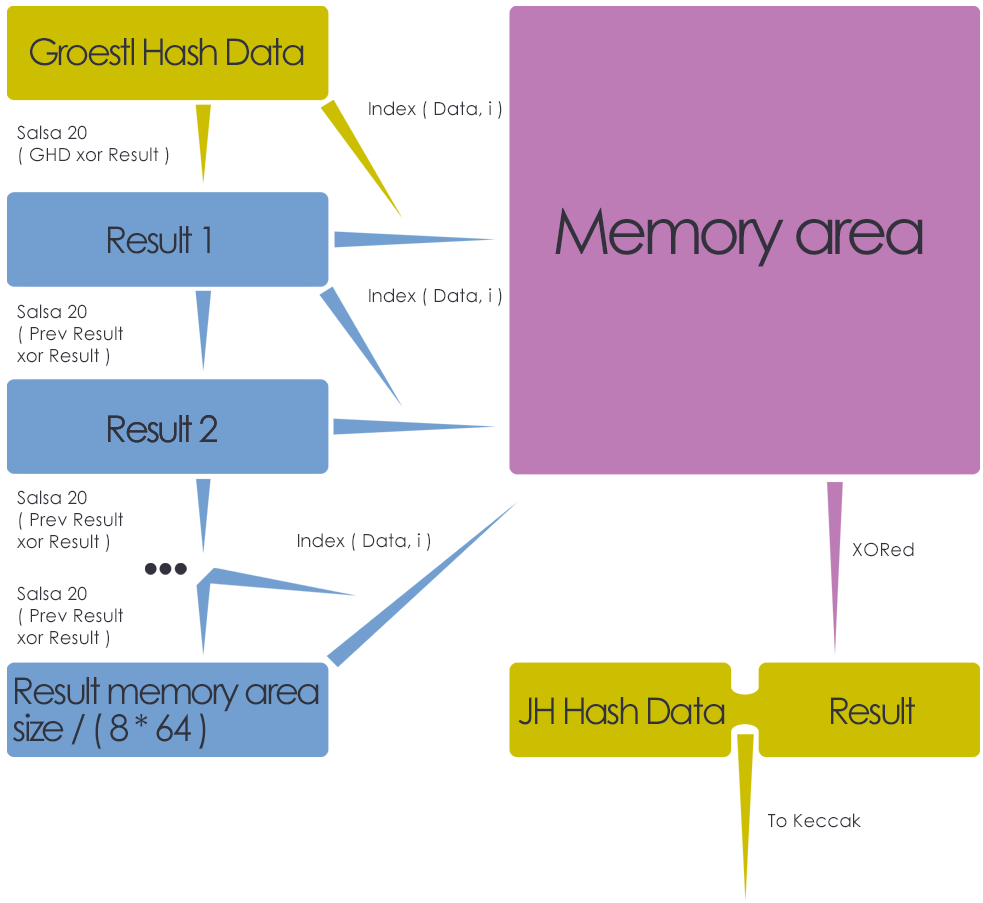
Сначала блок памяти размером 32 КБ для амплификации данных заполняется нулями, затем в него записываются данные, в псевдопроизвольные области в форме 512-битных блоков памяти. Salsa20 применяется последовательно: для каждого нового акта шифрования, используются результаты предыдущего акта, таким образом нет лёгкого метода для определения заранее того, где новый блок данных будет записан в памяти. Так память может обрабатываться только последовательно. Таким образом достигается невозможность распараллелить этот процесс на GPU и ASIC.
memset(aMemoryArea, 0, I_AMOUNT_OF_BYTES_FOR_MEMORY_HARD_FUNCTION);
Затем производятся последовательные шифрования промежуточного хэша блоков Бинариума (результат подфункции Skein):
for (i = 0; i < I_AMOUNT_OF_BYTES_FOR_MEMORY_HARD_FUNCTION / (64) / 2; i++) {
iWriteIndex = (
// % I_AMOUNT_OF_BYTES_FOR_MEMORY_HARD_FUNCTION here is to prevent
// integer overflow on subsequent addition operation.
GetUint64IndexFrom512BitsKey(uint1024CombinedHashes.begin() + 64, 0) % I_AMOUNT_OF_BYTES_FOR_MEMORY_HARD_FUNCTION + i * I_PRIME_NUMBER_FOR_MEMORY_HARD_HASHING) % (I_AMOUNT_OF_BYTES_FOR_MEMORY_HARD_FUNCTION - 8 * ECRYPT_BLOCKLENGTH);
// From previous encryption result in memory to next encryption result in memory.
ECRYPT_encrypt_blocks(&structECRYPT_ctx, uint1024CombinedHashes.begin() + 64, &(aMemoryArea[iWriteIndex]), 8);
uint1024CombinedHashes.XOROperator(64, &(aMemoryArea [iWriteIndex]));
}
Функция GetUint64IndexFrom512BitsKey () берёт 512-битный блок памяти (uint1024CombinedHashes.begin () + 64 ) и получает из него uint64_t-смещение для создания псевдопроизвольных индексов в 32-х КБ область aMemoryArea, которое затем объединяется с i * I_PRIME_NUMBER_FOR_MEMORY_HARD_HASHING, проводящими итерации по этой области памяти. Затем идёт процесс шифрования ECRYPT_encrypt_blocks () и его результаты объединяются с uint1024CombinedHashes.begin () + 64 , из которого на следующем шаге будут получены новые индекс и исходные данные. Это делает новые шифрующие шаги зависимыми от предыдущих и делает необходимым проведение шифрований последовательно. Также, при такой записи данных, трудно предсказать какие данные будут записаны в какие области памяти и добавляется большая вероятность перезаписи частей данных, поэтому очень трудно определить заранее, что окажется в конкретных битах памяти. После этого весь блок памяти хэшируется в 512-бит uint1024CombinedHashes.begin () + 64 с помощью операции XOR, которые затем комбинируются с результатом 5-го шага хэширования модифицированного X11 (результат подфункции JH).
for (i = 0; i < I_AMOUNT_OF_BYTES_FOR_MEMORY_HARD_FUNCTION / 64; i++) {
uint1024CombinedHashes.XOROperator(64, &(aMemoryArea[i * 64]));
}
Этот шаг происходит после применения 5-й хэширующей подфункции X11, перед применением подхэша Keccak.
При этом каждый подбор подходящего nNounce для блока может быть запущен в отдельном потоке, что открывает возможности для параллелизации. Но каждый поток требует его собственных 32-х КБ быстрой памяти для сохранения амплифицированных данных. Это лимитирует параллелизацию на GPU и увеличивает стоимость создания ASIC для криптовалюты Бинариум. Весь алгоритм также ограничен в скорости выполнения скоростью произвольных чтения и записи в оперативную память и кэши, что ограничивает его производительность на GPU и ASIC и открывает возможности для концепции egalitarian computing[10]: пользователи с оборудованием, обладающим разной производительностью, имеют равные или близкие возможности в сети. Это делает намного более трудным концентрацию больших вычислительных мощностей в одних руках и проведение атаки 51%[11].
2.2. Оценка производительности алгоритма.
Наш хэширующий алгоритм имеет 15 подфункций + 1 функцию, основанную на произвольных доступах к памяти. Из этих 15 только 3 конфигурируемые и в общем скорость хэширования лимитируется скоростью произвольных записи и чтения в оперативную память и кэши. По этому, мы ожидаем, что скорость хэширования не будет изменяться очень сильно, когда алгоритм реконфигурирует себя.
3. Внесение крупных изменений в архитектуру криптовалют, с сохранением текущего консенсуса
3.1. Алгоритм внесения крупных изменений в сеть криптовалюты в 4 шага
a). Реализация изменений в коде в неактивном состоянии и расположение хэширующих функций, которые позволяют клиентам определять обновились ли их пиры. Они делают это с помощью протокола подобного Протоколу доказательства с нулевым разглашением информации[12]: клиенты запрашивают у их пиров результаты применения хэширующих функций с определёнными индексами к произвольным данным и затем проверяют соответствие ответов со своими результатами. Также в код вносятся условия, которые определяют когда изменения будут активированы в сети (с какого номера блока или времени с Genesis-блока). Триггеры для этих условий запрашиваются у консенсуса RPC-серверов. Мы можем создать, скажем, 100 RPC-серверов, и сеть переключится на новую функциональность, только когда все сервера ответят и сообщат об одних и тех же условиях для переключения функциональности. Таким образом мы можем достаточно легко контролировать будет ли сеть переключаться или нет: мы можем отключить процесс обновления, в случае чрезвычайных происшествий, обесточив всего лишь 1 сервер. Злоумышленникам будет чрезвычайно трудно захватить контроль над всеми RPC-серверами и удерживать его в течение всего времени между установкой триггеров для условий переключения сети на новую функциональность и до самого переключения. Мы можем установить в программном обеспечении обязательную паузу между установкой триггеров и самим переключением в 1 неделю — несколько дней для того, чтобы обеспечить надёжность инициации проведения изменений только нами и никем больше.
b). Клиенты проверяют обновились ли пиры, с которыми они поддерживают связь, и «мягко» форсируют друг друга обновиться: отправляя GUI-нотификации об этом факте.
c). Клиенты «жёстко» форсируют друг друга обновиться: они заносят в бан других клиентов на определённое время, если они не обновили их программное обеспечение. Сеть перейдёт к этому шагу, когда количество обновившихся пиров достигнет 95% и больше. Клиенты могут собирать статистику об обновлениях их пиров и отправлять её главному RPC-серверу Бинариума. Мы можем рассматривать статистику только от клиентов, у которых есть минимальное количество Бинариума на счёте, так что злоумышленники не смогут создать большое количество пустых кошельков и пытаться искажать с их помощью статистику.
d). Само обновление: мы устанавливаем на консенсусе RPC-серверов условия для переключения, после которого сеть начнёт использовать новые функции (индекс блока, время с Genesis-блока и так далее). Клиенты получают эту информацию и переключаются, когда приходит время.
3.2. BIP'ы[16]
Мы можем рассмотреть возможность применения Bitcoin Improvements Proposals[16] для проведения обновлений сети. Но наша система более развита в этом направлении, так как BIP'ы требуют от авторов ручного получения консенсуса сети о проведении изменений и сохранении текущего консенсуса во время этого процесса, тогда как наша позволяет делать это автоматически.
Ссылки
- Публикация Bitcoin: https://bitcoin.org/bitcoin.pdf
- Dash: https://www.dash.org
- Публикация хэширующего алгоритма ГОСТ 2012 Стрибог: http://specremont.su/pdf/gost_34_11_2012.pdf
- Хэширующая функция Whirlpool: https://en.wikipedia.org/wiki/Whirlpool_(cryptography)
- Хэширующая функция SwiFFT: https://www.eecs.harvard.edu/~alon/PAPERS/lattices/swifft.pdf
- Блочная шифрующая функция ГОСТ 2015 Кузнечик: http://www.tc26.ru/standard/gost/GOST_R_3412-2015.pdf
- Блочная шифрующая функция ThreeFish: http://www.skeinhash.info/sites/default/files/skein1.3.pdf
- Блочная шифрующая функция Camellia: https://info.isl.ntt.co.jp/crypt/eng/camellia
- Поточный шифр Salsa20: https:/cr.yp.to/snuffle.html
- Egalitarian computing: https://arxiv.org/pdf/1606.03588.pdf
- Атака 51%: https://www.investopedia.com/terms/1/51-attack.asp
- Протокол доказательства с нулевым разглашением информации: https://en.wikipedia.org/wiki/Zero-knowledge_proof
- Пост-Квантовая Криптография: https://en.wikipedia.org/wiki/Post-quantum_cryptography
- Исходные коды Бинариума: https://github.com/binariumpay/binarium
- Быстрые Преобразования Фурье: https://en.wikipedia.org/wiki/Fast_Fourier_transform
- Bitcoin Improvements Proposals (BIP): https://github.com/bitcoin/bips/blob/master/bip-0002.mediawiki